皆さんこんにちは、TaroTechです。
今回はSPIの最難関分野である「推論についてその種類やコツについて」紹介していきます。
推論はSPIの高得点のカギを握っているともいわれているため対策必須の分野になります。
推論とは何か?ということや推論にはどんな種類の問題が出るのかということを押さえてしっかり対策を練っておきましょう。
1.推論とは?

推論とは、与えられた条件や情報から1つの答えまたは複数の答えを導く問題を指します。
主に就職活動におけるSPIの非言語分野において出題される問題になります。
問題の性質としては、数式を立てて答えを導く単純計算系というよりは、パターンを書き出しながらパズルに当てはめていくようなタイプになります。
時間を掛ければ答えにたどり着けるように、そこまで難解な問題というわけではありません。
しかし、限られた時間の中で正確に処理していくというのが推論の最大の難関ポイントになります。
また、普段から触れる機会の少ないタイプの問題になりますので、ある程度の「慣れ」が必要なのも推論の厄介なところになります。
推論はSPIにおいて頻出の分野でありかつSPIの高得点指標になる分野である
始めのうちは難しく感じても、たくさんの問題を解いていく中でしっかり対策して苦手意識をなくしておくことが就活や採用試験において非常に大事になってきます。
2.SPI推論のコツ・対策法

ここでは推論のコツや対策法について5つ紹介していきます。
2-1.問題パターンごとに解法を知る・覚える
コツ・対策法の1つ目は「問題パターンごとに解法を知る・覚える」です。
ひとえに推論と言ってもいくつかのパターンが存在します。
それぞれのパターンごとに解法や導出までの過程が異なります。それぞれの条件の正誤を判定する問題もあれば、当てはまるものをすべて選ばせるような問題もあります。
学習する過程でそれぞれの解法を知ってさらに覚えることで、問題を解くスピードを上げていくことが大事になります。
是非解法を自分のものにしていきましょう!
2-2.問題文に書かれた情報を式や図に書き起こして整理する
コツ・対策法の2つ目は「問題文に書かれた情報を式や図に書き起こして整理する」です。
推論を素早く正確に解く上でとても大事なのが、情報を整理するということになります。
推論では問題文に多くの情報が書かれており、その情報を基にパターンを書き出しながら問題を解いていくのが一般的です。
もし問題文から読み取ったことを頭だけで考えてしまうと途中でパターンがごちゃごちゃになって結局解けないということになりかねません。
そのため情報を整理して図や式に置き換えながら解答を考えるのが推論を攻略するコツになります。
勉強するときは2色のペンを使って情報を整理するのがおすすめ
推論の問題には1つの問の中で①と②が続いている「組問題」と呼ばれる問題が存在します。
このような問題では①で書きだしたパターンをさらに②で深掘りして答えを導くことになります。
こういった組問題を解く際に、それぞれの問題ごとに使用するペンの色を分けることで情報を色分けするということができます。
そうすることで色ごとに情報が整理され問題を解くスピードを自然と上げつつ正確に解く練習ができるのです。
2-3.学習するときは時間がかかってでも自力で答えまで導出する
コツ・対策法の3つ目は「学習するときは時間がかかってでも自力で答えまで導出する」です。
そもそも学習の時に自力で解くことができなければ、本番でも答えにたどり着くことは不可能です。
逆に言えば時間がかかってでも自力で答えを導き出せるということは、推論を解く能力は備わっているということになるので、後はスピードを上げる訓練をするだけということになります。
最初は模範解答に頼りながら答えまでの過程を真似してもいいので、少しずつ答えを見ないで解くという方式にシフトしていけるとよいでしょう。
このように練習でしっかり自分で解くという癖をつけておけば、本番で初見の問題が出ても、身に着けた解法通り答えを導いて高得点を得ることができるようになります。
2-4.SPIの学習時に電卓は使わない
コツ・対策法の4つ目は「学習時に電卓は使わない」ことです。
SPIの受験方式は、自宅で受験するWEBテスティング方式と外部の会場で受験するテストセンター方式の2種類に分けられます。
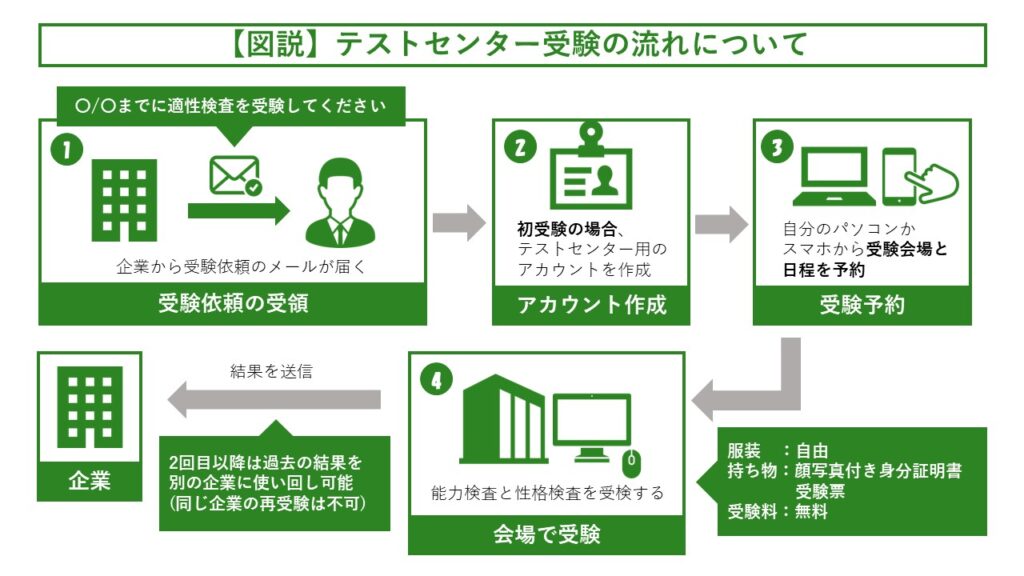
そのうちテストセンターでは、SPIを解く際に電卓を使用することが禁止されています。
このことから、SPIを学習するときは電卓を使わないで計算することに慣れておく必要があります。
ただ推論に関していうと、電卓を使用するほどの複雑な計算問題は出題されないので、他の分野と合わせて対策する際には電卓を使わない状況に慣れておくことが大事だという話です。
2-5.学習が進んだらひたすら問題演習と実践を積むこと
コツ・対策法の5つ目は「学習が進んだらひたすら問題演習と実践を積むこと」です。
結局のところ推論はたくさん問題を解いて慣れることが一番大事になります。
ある程度解法のインプットが終わったら、あとは問題集や実際にテストセンターで受験することをおすすめします。

私も問題集を買って徹底的にアウトプットをし続けていたら、いつの間にか推論が得意になっていました。
【おすすめ問題集】
どちらか1冊を買って何周か問題を解くことを推奨します。
【おすすめのサービス】
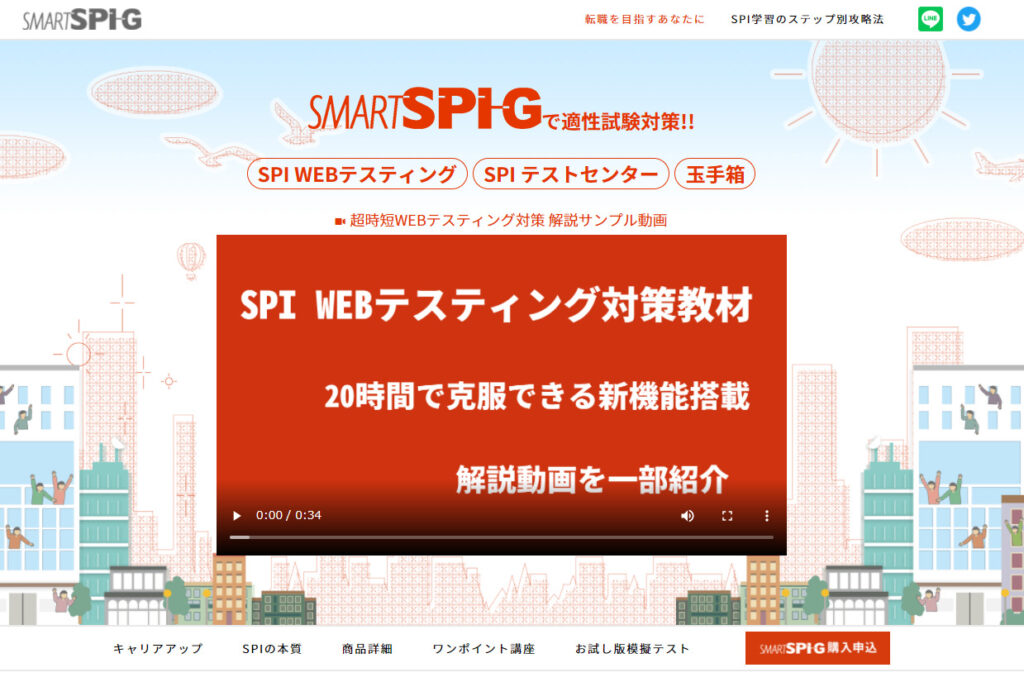
おすすめ度:
費用:2500円/6か月
SMART/SPI-Gでは、SPIを実際に自分のパソコンやスマホから本番さながらに演習することができるサービスになります。
メインターゲットは第二新卒ですが、ラインナップはSPIだけでなく玉手箱も含まれているため新卒就活生にもおすすめです。就活仲間と割り勘して半年間問題演習するとよいでしょう。
4.SPI非言語における推論の種類と問題

推論にはいくつかの問題の種類が存在し、それぞれ解き方が異なります。
| 種類 | 重要度 |
|---|---|
| 正誤判断 | |
| 順番推理 | |
| 内訳推理 | |
| 平均推理 | |
| 密度・濃度 | |
| 勝ち負け | |
| 位置関係 | |
| チェックボックス | |
| 数値推理 |
このように推論の中にもいくつか種類があるのでひとつずつ例題を見ていきましょう。
正誤判断
正誤判断では、各条件同士の正誤の関係性を判定していきます。
それでは例題を見ていきましょう。
数色のカードがある。これらのカードについて、次のような発言があった。
P 赤いカードが3枚、青いカードが4枚、緑のカードが4枚ある。
Q カードは少なくとも9枚ある。
R 赤、青、緑のカードが少なくとも3枚ずつ入っている。
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければRも必ず正しい
イ Qが正しければPも必ず正しい
ウ Rが正しければQも必ず正しい
②次の推論のうち正しいものはどれか。
カ Pが正しければQも必ず正しい
キ Qが正しければRも必ず正しい
ク Rが正しければPも必ず正しい
推論の中では比較的優しい問題に分類され、主に非言語の序盤に出題されます。
確実に取りたい問題になるのでしっかり対策をしましょう。
順番推理
順番推理は、条件から推理される順番を求める問題になります。
それでは例題を見ていきましょう。
P、Q、R、Sの4人がテストを受けた。4人の得点についてア、イ、ウが分かっているとき、4人の得点を高い順に並べたものはどれか。
ア Rの得点はPとQの得点の平均に等しい
イ SはPより得点が高いが、1位ではない
ウ Qの次に点が高いのはRではなくSである
A QSRP
B RQSP
C QSPR
D RSPQ
こちらも頻出の問題になりますが、パターンを書き出す必要があるため比較的難しい問題に分類されます。
パターンを抜け漏れなく書き出すという作業に慣れておきましょう。
内訳推理
内訳推理は、条件から数値の配分を推理していく問題です。
それでは例題を見ていきましょう。
黒、赤、青のボールペンを、それぞれ1本以上、合計で15本買った。15本の内訳について、次のことが分かっている。
Ⅰ) 黒のボールペンは5本以上買った。
Ⅱ) 赤のボールペンと青のボールペンの差は3本である。
次の推論のうち、確実に正しいと言えるものはどれか。
ア 黒のボールペンの本数は偶数である。
イ 黒のボールペンが6本ならば、赤のボールペンは6本である。
ウ 赤のボールペンが5本ならば、黒のボールペンは8本である。
この問題では代入を頻繁に行いますが、その代入法に少しコツがいる点がこの問題の特徴です。こちらも比較的難しい問題に分類されるためしっかり対策しておきましょう。
平均推理
平均推理は、名前の通り平均値や平均に関する正誤を判定する問題になります。
それでは例題を見ていきましょう。
食品店で3種類の商品P、Q、Rの在庫を調べたところ、次のことが分かった。
Ⅰ) P、Q、Rの在庫数の平均は184個である。
Ⅱ) P、Qの在庫数の平均は205である。
Ⅲ) P、Rの在庫数の平均は192個である。
①Qの在庫数はいくつか?
A 121個
B 142個
C 168個
D 197個
E どれでもない
②Ⅰ)~Ⅲ)以外に商品S、Tの在庫数の平均が276個であることが分かった。次の推論のうち確実に正しいと言えるものはどれ?
ア 5つの商品のうち最も在庫が少ないのはRである。
イ 5つの商品のうち、最も在庫の多いのはS、Tのいずれか、または両方である。
ウ Pの在庫数よりQ、S、Tの在庫数の平均の方が多い。
平均は公式さえ覚えてしまえばそこまで難しくはありませんが、時折ひっかけ問題が出題されるため少し注意が必要な問題になります。
濃度・密度
濃度・密度では、名前の通り密度・濃度の数値やそれに関する正誤を導出します。
それでは例題を見ていきましょう。
次の表は、P市、Q市、R市の人口密度(1km^2当たりの人口)である。P市とQ市の面積は等しく、それぞれR市の面積の半分である。
| 市 | 人口密度(人/km^2) |
|---|---|
| P市 | 420 |
| Q市 | 340 |
| R市 | 250 |
①次の推論のア、イの正誤について答えよ。
ア P市の人口はR市の人口より多い。
イ P市とR市を合わせた地域の人口密度はQ市と等しい。
②次の推論のカ、キの正誤について答えよ。
カ Q市とR市の人口の和は、P市の人口の2倍である。
キ Q市とR市を合わせた地域の人口密度は、P市の人口密度の2倍である。
こちらも平均同様公式を覚えればそこまで難しくないもんだばかりなので、はやめに対策しておきましょう。
勝ち負け
勝ち負けでは、問題文から勝敗に関する各条件の正誤を判定します。
それでは例題を見ていきましょう。
P、Q、Rの3人がじゃんけんをした。1回目は勝負がつかず、2回目は1人が勝った。このじゃんけんについて次のことが分かっている。ただし、あいことは3人とも同じ手を出したか、3人とも違う手を出したかのどちらかである。
Ⅰ) Pは2回ともチョキを出した。
Ⅱ) Qは1回だけパーを出した。
Ⅲ) Rは1回目にグーを出した。
2回目のじゃんけんについて、次の推論ア、イ、ウのうち必ずしも誤りではないものはどれか。
ア 勝ったのはPである
イ 勝ったのはQである
ウ パーを出した人が少なくとも1人はいる
勝ち負けの問題では主に対戦表とトーナメント表を書いて問題を解いていくため、それぞれのパターンに沿った考え方を身に着けておく必要があります。
比較的難しい問題に分類されるため時間をかけて対策を練っておくとよいでしょう。
位置関係
位置関係では、条件からパターンを書き出して問題文の正誤を判定します。
それでは例題を見ていきましょう。
図のような2階建てのアパートにP・Q・R・S・T・Uの6人が一人一部屋ずつ住んでいる。空き部屋は各階に1部屋ずつあり、6人の部屋割りについて以下のことが分かっている。
| 201 | 202 | 203 | 204 |
| 101 | 102 | 103 | 104 |
Ⅰ) 202号室は空き部屋である
Ⅱ) PはSの隣に住んでいる
Ⅲ) Pの真下にはQが住んでいる
Ⅳ) Tは端に住んでおらず、一方の隣は空き部屋である
①次の推論ア、イ、ウのうち必ずしも誤りではないものはどれか。
ア RはUの隣に住んでいる
イ 空き部屋の真下も空き部屋である
ウ Tは1階に住んでいる
②最も少ない情報で全員の部屋割りが分かるには、情報のⅠ~Ⅳのほかにどの情報を加えればいいか?
カ Rの真下は空き部屋である
キ Rは端に住んでいる
ク Uは103号室に住んでいる
位置関係は情報が複雑になりがちなため、解答までのプロセスが長くなりやすい問題になります。
推論の中でも解答にたどり着くのが大変な問題が多い傾向にあるため対策は必須です。
チェックボックス
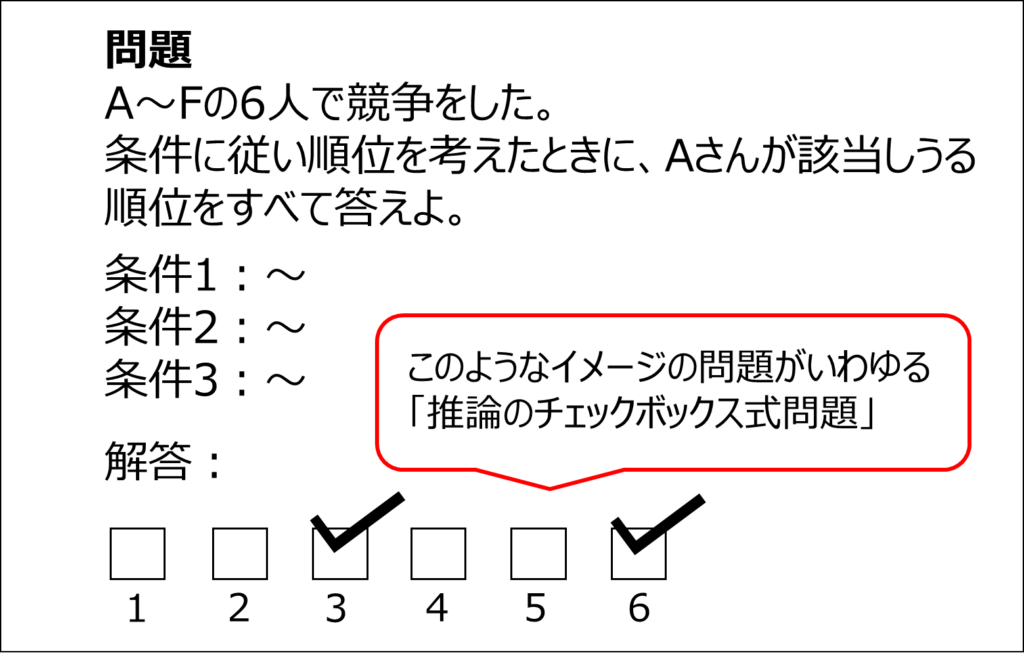
SPI推論におけるチェックボックスとは、条件から問題文に当てはまるものをすべて選ばせる問題になります。
上図のように選択肢がチェックボックスになっていることからこの名前がついています。
それでは例題を見ていきましょう。
ある歌手が1~6月の間に全国の会場でコンサートを行った。これらのコンサートについて次のことが分かっている。
Ⅰ) コンサートは1か月に少なくとも1回以上3回以下の頻度で行われた。
Ⅱ) 2月は1回だけしか行われなかった。
①合計15回のコンサート行う場合、10回目のコンサートは何月に行われる可能性があるか?
□ 1月 □ 2月 □ 3月 □ 4月 □ 5月 □ 6月
②合計10回のコンサート行う場合、5回目のコンサートは何月に行われる可能性があるか?
□ 1月 □ 2月 □ 3月 □ 4月 □ 5月 □ 6月
チェックボックスでは解答に当てはまるものを抜け漏れなくすべて書き出す必要があります。
そのため解答に抜け漏れがあったり逆に余計なものを1つでも選んでいたら解答としては「×」になります。
またチェックボックスはテストセンターで出題された時の高得点目安としても知られているため、本番では確実に取りたい問題でもあります。
SPIの中では最難関の問題になりますので、多くの問題を解いて慣れていくことをおすすめします。
数値推理
数値推理は、基本的な四則演算を用いて□に当てはまる数値を求めます。
それでは例題を見ていきましょう。
空欄に当てはまる数値を答えなさい。
Xは2の倍数、Yは3の倍数、Zは5の倍数であり、以下のことが分かっている。
ア X+Z=42
イ Y+Z=38
X、Y、Zがいずれも正の整数であるとき、Xは□である。
こちらの問題については推論以外の分野の対策をすれば同時に対策ができるため、推論の中ではそこまで優先度は高くありません。
ただ、SPIの本番ではほぼ確実に出題される問題になるため、確実に取り切れるよう計算練習をしておくことをおすすめします。
まとめ
皆さんいかがだったでしょうか?
今回は「推論の種類やコツ・対策法」について紹介してきました。
推論は問題によって内容や対策法が異なります。
就活全体を通してもSPIの対策は非常に重要なタスクになるため、早いうちから推論の対策をしておくと適性検査落ちを防ぐことができます。
明日からでもしっかり勉強していきましょう!








コメント