皆さんこんにちは、TaroTechです。
今回はシリーズ第1弾ということで、「推論(正誤判断)の解法テクニック」について例題付きで紹介していきます。
推論はSPIの中でも最重要項目であるため難易度もそれなりに高く、SPIの高得点のカギを握っているともいわれているため対策必須の分野になります。
この記事では苦手な人でも解法を自分のものにできるよう、実際に私が解く際に使っているメモ書きを解説として掲載しています。
是非この機会に苦手を克服していきましょう!
1.推論とは?

推論とは、与えられた条件や情報から1つの答えまたは複数の答えを導く問題を指します。
主に就職活動におけるSPIの非言語分野において出題される問題になります。
問題の性質としては、数式を立てて答えを導く単純計算系というよりは、パターンを書き出しながらパズルに当てはめていくようなタイプになります。
時間を掛ければ答えにたどり着けるように、そこまで難解な問題というわけではありません。
しかし、限られた時間の中で正確に処理していくというのが推論の最大の難関ポイントになります。
また、普段から触れる機会の少ないタイプの問題になりますので、ある程度の「慣れ」が必要なのも推論の厄介なところになります。
推論はSPIにおいて頻出の分野でありかつ高得点のカギを握る分野である
始めのうちは難しく感じても、たくさんの問題を解いていく中でしっかり対策して苦手意識をなくしておくことが就活や採用試験において非常に大事になってきます。
2.推論全般の対策・攻略法

ここでは推論全般の対策や攻略法について解説していきます。
2-1.問題パターンごとに解法を知る・覚える
対策・攻略法の1つ目は「問題パターンごとに解法を知る・覚える」です。
ひとえに推論と言ってもいくつかのパターンが存在します。
| 種類 | 重要度 |
|---|---|
| 正誤判断 | |
| 順番推理 | |
| 内訳推理 | |
| 平均推理 | |
| 密度・濃度 | |
| 勝ち負け | |
| 位置関係 | |
| チェックボックス | |
| 数値推理 |
このように推論にはいくつかの問題パターンが存在し、問題ごとに解法や導出までの過程が異なります。それぞれの条件の正誤を判定する問題もあれば、当てはまるものをすべて選ばせるような問題もあります。
学習する過程でそれぞれの解法を知ってさらに覚えることで、問題を解くスピードを上げていくことが大事になります。
是非解法を自分のものにしていきましょう!
2-2.問題文に書かれた情報を式や図に書き起こして整理する
対策・攻略法の2つ目は「問題文に書かれた情報を式や図に書き起こして整理する」です。
推論を素早く正確に解く上でとても大事なのが、情報を整理するということになります。
推論では問題文に多くの情報が書かれており、その情報を基にパターンを書き出しながら問題を解いていくのが一般的です。
もし問題文から読み取ったことを頭だけで考えてしまうと途中でパターンがごちゃごちゃになって結局解けないということになりかねません。
そのため情報を整理して図や式に置き換えながら解答を考えるのが推論を攻略するコツになります。
勉強するときは2色のペンを使って情報を整理するのがおすすめ
推論の問題には1つの問の中で①と②が続いている「組問題」と呼ばれる問題が存在します。
このような問題では①で書きだしたパターンをさらに②で深掘りして答えを導くことになります。
こういった組問題を解く際に、それぞれの問題ごとに使用するペンの色を分けることで情報を色分けするということができます。
そうすることで色ごとに情報が整理され問題を解くスピードを自然と上げつつ正確に解く練習ができるのです。
2-3.学習するときは時間がかかってでも自力で答えまで導出する
対策・攻略法の3つ目は「学習するときは時間がかかってでも自力で答えまで導出する」です。
そもそも学習の時に自力で解くことができなければ、本番でも答えにたどり着くことは不可能です。
逆に言えば時間がかかってでも自力で答えを導き出せるということは、推論を解く能力は備わっているということになるので、後はスピードを上げる訓練をするだけということになります。
最初は模範解答に頼りながら答えまでの過程を真似してもいいので、少しずつ答えを見ないで解くという方式にシフトしていけるとよいでしょう。
このように練習でしっかり自分で解くという癖をつけておけば、本番で初見の問題が出ても、身に着けた解法通り答えを導いて高得点を得ることができるようになります。
2-4.学習が進んだらひたすら問題演習と実践を積むこと
対策・攻略法の4つ目は「学習が進んだらひたすら問題演習と実践を積むこと」です。
結局のところ推論はたくさん問題を解いて慣れることが一番大事になります。
ある程度解法のインプットが終わったら、あとは問題集や実際にテストセンターで受験することをおすすめします。

私も問題集を買って徹底的にアウトプットをし続けていたら、いつの間にか推論が得意になっていました。
【おすすめ問題集】
どちらか1冊を買って何周か問題を解くことを推奨します。
【おすすめのサービス】
おすすめ度:
費用:2500円/6か月
SMART/SPI-Gでは、SPIを実際に自分のパソコンやスマホから本番さながらに演習することができるサービスになります。
メインターゲットは転職者ですが、ラインナップはSPIだけでなく玉手箱も含まれているため就活生にもおすすめです。就活仲間と割り勘して半年間問題演習するとよいでしょう。
4.推論(正誤判断)の例題と解答
この記事では推論(正誤判断)の例題と解答を紹介していきます。
まず自力で問題を解いてみよう!
例題
【問1】
数色のカードがある。これらのカードについて、次のような発言があった。
P 赤いカードが3枚、青いカードが4枚、緑のカードが4枚ある。
Q カードは少なくとも9枚ある。
R 赤、青、緑のカードが少なくとも3枚ずつ入っている。
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければRも必ず正しい
イ Qが正しければPも必ず正しい
ウ Rが正しければQも必ず正しい
②次の推論のうち正しいものはどれか。
カ Pが正しければQも必ず正しい
キ Qが正しければRも必ず正しい
ク Rが正しければPも必ず正しい
【問2】
1~50の数が書かれた50枚のカードがある。この中から2枚のカードを同時に選ぶとき、2枚のカードの合計について以下の発言があった。
P 2つの数の和は偶数だった
Q 2つの数の和は8の倍数だった
R 2つの数の和を4で割ると余りが0だった。
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければQも必ず正しい
イ Qが正しければRも必ず正しい
ウ Rが正しければPも必ず正しい
②次の推論のうち正しいものはどれか。
カ Pが正しければRも必ず正しい
キ Qが正しければPも必ず正しい
ク Rが正しければQも必ず正しい
【問3】
数学、英語、国語の3科目のテスト結果について、次のような3通りの発言があった。
P 3科目の平均は60点以上だった
Q 成績は3科目とも60点以上だった
R 数学が60点、英語が70点、国語が65点だった。
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければRも必ず正しい
イ Qが正しければPも必ず正しい
ウ Rが正しければQも必ず正しい
②次の推論のうち正しいものはどれか。
カ Pが正しければQも必ず正しい
キ Qが正しければRも必ず正しい
ク Rが正しければPも必ず正しい
【問4】
10円、50円、100円の効果がそれぞれ何枚かある。これらについて以下の発言があった。
P 100円が1枚、50円が3枚、10円が5枚ある。
Q 硬貨の合計枚数は9枚ある
R 合計金額は300円である
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければQも必ず正しい
イ Qが正しければRも必ず正しい
ウ Rが正しければPも必ず正しい
②次の推論のうち正しいものはどれか。
カ Pが正しければRも必ず正しい
キ Qが正しければPも必ず正しい
ク Rが正しければQも必ず正しい
【問5】
さいころを2個同時に振ったときの出目について、以下の発言があった。
P 出た目の和が7
Q 出た目の差が1か2
R 出た目は3と4だった
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければQも必ず正しい
イ Qが正しければRも必ず正しい
ウ Rが正しければPも必ず正しい
②次の推論のうち正しいものはどれか。
カ Pが正しければRも必ず正しい
キ Qが正しければPも必ず正しい
ク Rが正しければQも必ず正しい
解答
問1. ①アとウ ②カ
問2. ①イとウ ②キ
問3. ①イとウ ②ク
問4. ①ア ②カ
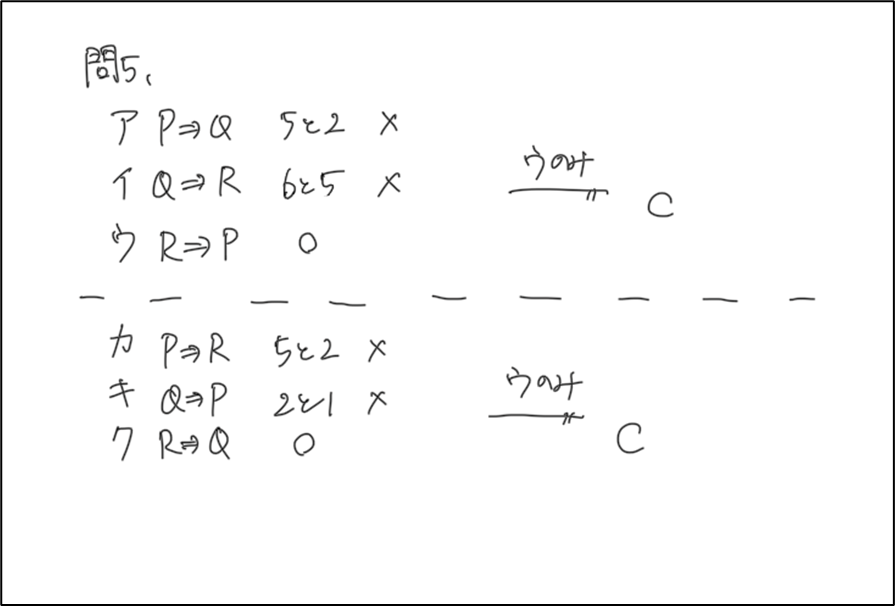
問5. ①ウ ②ウ


5.推論(正誤判断)の解法テクニック

それでは最後に推論(正誤判断)の解法テクニックについて紹介します。
反例をさがす
正誤判断問題では「〇が正しければ△も必ず正しい」ということの正誤を判定します。
この問題を解く際に必ず押さえてほしい解法が「反例探し」になります。
そもそも反例とは条件に当てはまらない場合のことを指します。
正誤判断問題ではこの反例がないかを素早く判断することが大事になります。
もし1つでも反例を見つけることができればその条件は一瞬で「誤」と判断することができます。
反例を探すときは極端な例を考えてみると早い
例えば例題の問4のウの場合だと、
【問4】
10円、50円、100円の効果がそれぞれ何枚かある。これらについて以下の発言があった。
P 100円が1枚、50円が3枚、10円が5枚ある。
Q 硬貨の合計枚数は9枚ある
R 合計金額は300円である
以上の発言が、必ずしも正しいとは限らないとする。
①次の推論のうち正しいものはどれか。
ア Pが正しければQも必ず正しい
イ Qが正しければRも必ず正しい
ウ Rが正しければPも必ず正しい
「合計金額が300円なら100円が1枚、50円が3枚、10円が5枚となる。」と言い換えることができます。
この条件に対する反例の一つは「10円が30枚の時」が挙げられます。
今回の問題では特に枚数の指定がないため、このような極端なものも反例として挙げられます。
何度も演習する中でこの反例を見つけるという作業をすぐにできるようにしましょう。
条件の包含関係を理解する
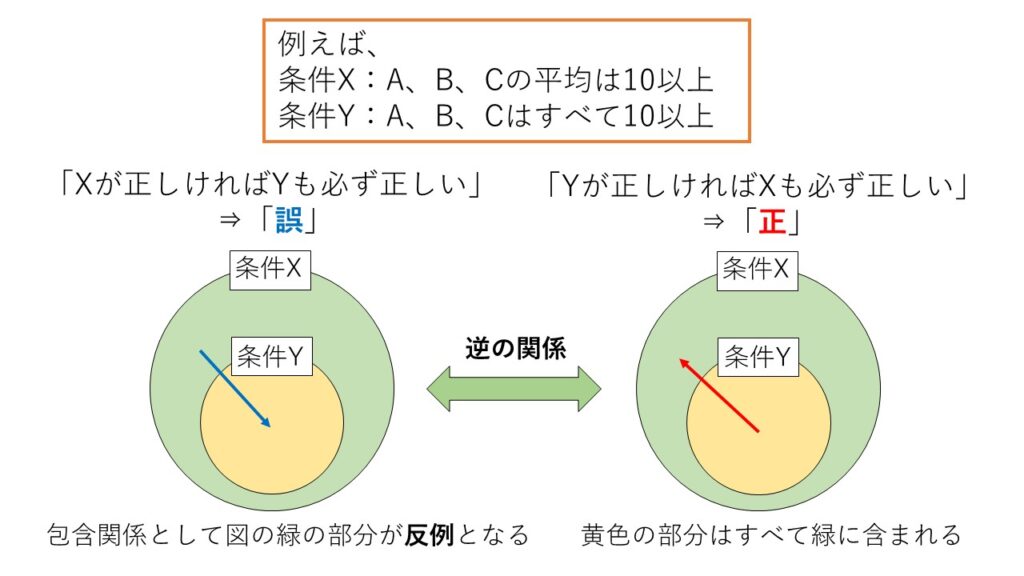
推論の正誤判断では、それぞれの条件同士の包含関係を理解することが大事になります。
図の例のように条件が2つあった場合に、どちらがどちらにすべて含まれているかを図式化すると条件を理解しやすくなります。
高校数学の命題という分野に関わってくる話ですが、包含関係の内側から外側に矢印が向く場合はその条件は「真」になります。(図だとY⇒Xのこと)
一つ時短テクニックを紹介しておくと、A⇒Bが「〇」だった場合、問題文を読まなくてもB⇒Aは「×」と確定できます。これは上図のように包含関係を図式化すれば明らかです。
(ただしA⇒Bが「×」のときはその逆が×か〇かは確定しないので注意してください。)
本番では図式化すると時間が足りなくなる可能性があるので「反例探し」をおすすめしますが、家庭学習するときは理解度を確かめるためにも図式化してみてもいいかもしれません。
まとめ
皆さんいかがだったでしょうか?
今回は推論の攻略法~正誤判断編~ということで、例題とともに解法テクニックを紹介してきました。
推論は始めは難しくても、学習を積み重ねているうちに少しずつ問題に慣れてきます。
ぜひ今回紹介した解法テクニックを駆使して高得点を狙っていきましょう!



コメント